半加算器で全加算器を作る

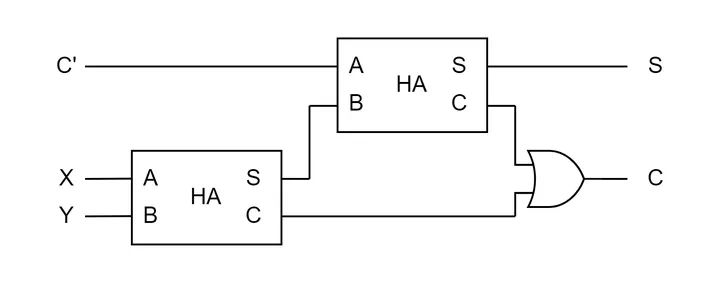
全加算器はサムネイルのように半加算器二つで実装できます。ですが図のシンプルさに対して、その導出過程がなかなかムズイので、メモしておきます。

論理式から導出

まずは半加算器の定義を確認します。半加算器は入力 A, B に対して、出力 S (和), C (桁上げ) を出力します。なお $\oplus$ は XOR です。

$$ \begin{align*} \text{半加算器}(A, B) & = (S_{HA}, C_{HA}) \\ S_{HA} & = A \oplus B \\ C_{HA} & = A B \end{align*} $$

全加算器は 入力 X, Y, C’ (下位加算器からの桁上げ) に対して、S, C を出力します。次の式は真理値表をもとに、カルノー図を使って簡略化したものです。

$$ \begin{align*} \text{全加算器}(X, Y, C') & = (S_{FA}, C_{FA}) \\ S_{FA} & = \bar{X} \bar{Y} C' + \bar{X} Y \bar{C'} + X Y C' + X \bar{Y} \bar{C'} \\ C_{FA} & = X Y + X C' + Y C' \\ \end{align*} $$

$S_{FA}$ , $C_{FA}$ を $S_{HA}$, $C_{HA}$ で表すことができれば、全加算器を半加算器で実装できることになります。

まずは $S_{FA}$ から。

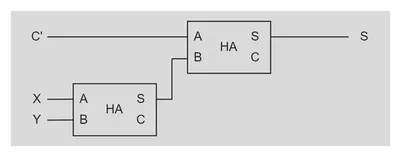
$$ \begin{align*} S_{FA} & = \bar{X} \bar{Y} C' + \bar{X} Y \bar{C'} + X Y C' + X \bar{Y} \bar{C'} \\ & = C' (\bar{X} \bar{Y} + X Y) + \bar{C'} (\bar{X} Y + X \bar{Y}) \\ & = C' (\overline{ X \oplus Y}) + \bar{C'} (X \oplus Y) \\ & = C' \oplus X \oplus Y \\ & = S_{HA} (S_{HA}(X, Y), C') \end{align*} $$

この式は次のように解釈できます。

次に $C_{FA}$ です。これがムズイというか、恣意的な変形が必要です。

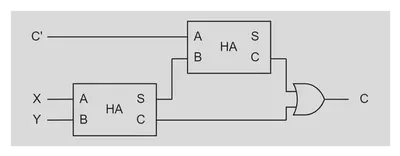
$$ \begin{align*} C_{FA} & = X Y + X C' + Y C' \\ & = X Y + X C' + X Y + Y C' \\ & = X (Y + C') + Y (X + C') \\ & = X (Y + \bar{Y} C') + Y (X + \bar{X} C') \\ & = XY + X \bar{Y} C' + Y \bar{X} C' \\ & = XY + C' (X \bar{Y} + Y \bar{X}) \\ & = XY + C' (X \oplus Y) \\ & = C_{HA}(X, Y) + C_{HA}(S_{HA}(X, Y), C') \\ \end{align*} $$

この式は次のように解釈できます。

直感的理解

式変形してカチカチにやってもいいですが、テスト以外で導出するのは流石にやりたくないですし、導出結果をあらかじめイメージできると見直しやすいと思ったので、直感的に理解できるような説明をしておきます。

全加算器は言い換えると 3bit 加算器です。3bit の和は、2bit を加算した結果を残りの 1bit と加算することで求められるので、和の信号は次のようなイメージになります。

桁上げが発生する条件は、3bit のうち 2bit 以上が 1 の場合です (011, 101, 111 とか)。2bit 以上が 1 になるときには、必ずどちらかの半加算器が桁上げするので、半加算器の桁上げ信号の論理和をとってあげればよいです。次のようなイメージになります。