ボーアの原子モデル

ボーアの原子モデル
授業でやったのでまとめました。
ボーアの原子モデルとは、サムネのような原子核の周りを電子がくるくる回るというモデルです。また回るときの軌道は決まっており、好きな軌道半径には存在できないとしています。これはボーアのモデル以前に存在した、ラザフォードの原子モデルもおなじです。
ただ、ラザフォードの原子モデルには、円運動する電子は電磁波を放出しながら原子核へ落ちるという問題がありました。しかし原子は安定して存在できています。ボーアはこの矛盾を回避するために量子条件と振動数条件という仮定を導入し、モデルを構築しました。このモデルは水素原子の発光スペクトルを上手く説明できたため、受け入れられました。
🌟 量子条件
電子が次の式に示す軌道に存在する場合、加速運動をしていても電子がエネルギーを放出しないと仮定します。
$$ rmv=\frac{h}{2\pi}n \quad (n=1,2,3,\ldots) \\ \\[1em] \begin{aligned} r &: \text{電子の軌道半径} \\ m &: \text{電子の質量} \\ v &: \text{電子の速度} \\ h &: \text{プランク定数} \\ \end{aligned} $$重要なのは、あくまで仮定であり、加速運動をする電子がエネルギーを放出しない理由は説明されていないという点です。
謎だったので先生に聞いたところ、あくまでモデルであり現象を説明できればよく、厳密さを求めていくとそこに答えはないそうです。球形の牛がこんなところにもいました。
🌟 振動数条件
軌道間を遷移する場合、エネルギーを放出または吸収し、そのエネルギーは次の式で表されます。
$$ h\nu = E_m - E_n \\[1em] \begin{aligned} h &: \text{プランク定数} \\ \nu &: \text{放出または吸収される電磁波の周波数} \\ E_m &: \text{電子が軌道 $m$ のときのエネルギー} \\ E_n &: \text{電子が軌道 $n$ のときのエネルギー} \\ \end{aligned} $$軌道、エネルギーは飛び飛びになる
仮定(1) が成り立つとして電子の軌道半径、エネルギーを計算すると、各値は連続な値をとれず離散的な値になることが示されます。実際に計算してみます。
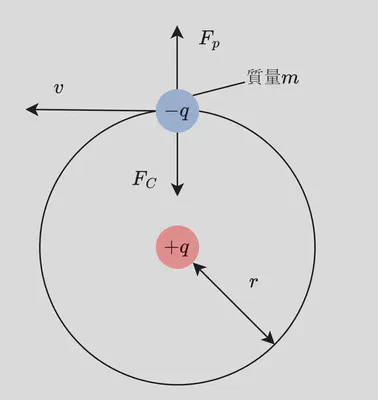
🌟 軌道半径を求める
遠心力とクーロン力が釣り合っている事を利用して、電子の軌道半径 $r$ を求めます。
遠心力 $F_P$ とクーロン力 $F_C$ は、それぞれ次のように表せます。原子の内部は真空とし、誘電率は $\varepsilon_0$ とします。
$$ F_P=\frac{mv^2}{r} \\ \\[1em] \begin{aligned} F_C &= \frac{|+q||-q|}{4\pi\varepsilon_0r^2} \\[1em] &= \frac{q^2}{4\pi\varepsilon_0r^2} \tag{1.1} \end{aligned} $$電子は円運動をしており、遠心力とクーロン力は等しいため、
$$ F_P=F_C \\ \\[1em] \frac{mv^2}{r}=\frac{q^2}{4\pi\varepsilon_0r^2} \tag{1.2} $$半径 $r$ について解くと、
$$ r=\frac{q^2}{4\pi\varepsilon_0mv^2} \tag{1.3} $$となります。ここで仮定(1)を $v$ について変形します。
$$ v=\frac{h}{2\pi rm}n \quad (n=1,2,3,\ldots) $$式 $(1.3)$ に代入すると、
$$ r=\frac{\varepsilon_0 h^2}{mq^2}n^2 \quad (n=1,2,3,\ldots) \tag{1.4} $$よって電子の軌道半径は離散的に定まることを示せました。
🌟 エネルギーを求める
電子の持つエネルギーとは、運動エネルギーとクーロンポテンシャルエネルギーの和です。
クーロンポテンシャルエネルギーは電子をクーロン力によって無限遠点から $r$ まで持ってくるのに必要なエネルギーです。
まずは運動エネルギーを求めます。運動エネルギーは次のように表されます。
$$ E_K=\frac{1}{2}mv^2 \tag{2.1} $$式 $(1.2)$ を $v^2$ について変形し、式 $(2.1)$ に代入すると、
$$ v^2=\frac{q^2}{4\pi\varepsilon_0mr}\\ \\[1em] \begin{aligned} E_K &= \frac{1}{2}m\left(\frac{q^2}{4\pi\varepsilon_0mr}\right) \\ &= \frac{q^2}{8\pi\varepsilon_0r} \end{aligned} $$次にクーロンポテンシャルエネルギーを求めます。原子核と電子の間に働くクーロン力は式 $(1.1)$ で表せます。無限遠点から $r$ まで持ってくるのに必要なエネルギーは、クーロン力を $r$ まで積分することで求めることができます。
$$ \begin{aligned} E_C &= \int_{\infty}^{r}F_Cdr \\[1em] &= \int_{\infty}^{r}\frac{q^2}{4\pi\varepsilon_0r^2}dr \\[1em] &= \frac{q^2}{4\pi\varepsilon_0} \int_{\infty}^{r}\frac{1}{r^2}dr \\[1em] &= \frac{q^2}{4\pi\varepsilon_0}\left[-\frac{1}{r}\right]_{\infty}^{r} \\[1em] &= -\frac{q^2}{4\pi\varepsilon_0r} \end{aligned} $$よって、電子の持つエネルギーは次のように表されます。
$$ \begin{aligned} E &= E_K+E_C \\[1em] &= \frac{q^2}{8\pi\varepsilon_0r}-\frac{q^2}{4\pi\varepsilon_0r} \\[1em] &= -\frac{q^2}{8\pi\varepsilon_0r} \end{aligned} $$式 $(1.4)$ を代入すると、
$$ \begin{aligned} E &= -\frac{q^2}{8\pi\varepsilon_0 \frac{\varepsilon_0 h^2}{mq^2}n^2} \quad (n=1,2,3,\ldots)\\[1em] &= -\frac{m q^4}{8\pi\varepsilon_0^2 h^2} \frac{1}{n^2} \quad (n=1,2,3,\ldots) \tag{2.2} \end{aligned} $$よって、電子の持つエネルギーは離散的に定まることを示せました。
🌟 物質波
物質波の考えを用いて軌道半径の離散性を説明することもできます。またこんど
水素原子の発光スペクトルを説明できるか
🌟 水素のスペクトル
何かしらの原子で満たされた空間に電場等のエネルギーを加えると、原子中の電子が励起され、電子が高いエネルギー準位に遷移します(電子が電子軌道を遷移する)。その後、電子は元のエネルギー準位に戻るときにエネルギー(電磁波)を放出します。この電磁波を分光器で観測すると、原子固有の波長の光が観測されます。これが発光スペクトルです。
発光スペクトルはいくつかの波長の輝線からなり、ボーアの原子モデルが構築される以前から、各波長は次の式で表されることが知られていました。
$$ \begin{aligned} \frac{1}{\lambda} &= R\left( \frac{1}{m^2}-\frac{1}{n^2} \right) \\ & \quad (m=1,2,3、n=m+1,m+2,\ldots) \tag{3.1} \end{aligned} $$$R$ はリュードベリ定数。今からこれを仮定を用いて求めます。
🌟 やること
仮定(2) を用いて、水素原子の軌道遷移時のエネルギーを計算し、リュードベリ定数 $R$ を求めます。
リュードベリ定数は実験的に求められた値で、仮定(2) を用いて求めた値と一致すれば、ボーアの原子モデルが水素原子の発光スペクトルを説明できることになります。
🌟 電磁波の波長を求める
仮定(2) と式 $(2.2)$ を用いて、水素原子から放出される電磁波の振動数を求めます。
$$ \begin{aligned} h\nu &= E_m - E_n \\[1em] \nu &= \frac{1}{h} \left( -\frac{m q^4}{8\pi\varepsilon_0^2 h^2} \frac{1}{m^2} +\frac{m q^4}{8\pi\varepsilon_0^2 h^2} \frac{1}{n^2} \right) \tag{3.2} \\ &\quad (m=1,2,3、n=m+1,m+2,\ldots) \end{aligned} $$また、波長 $\lambda$ と振動数 $\nu$ と光速 $c$ には次の関係があるので、
$$ \lambda = \frac{c}{\nu} \tag{3.3} $$式 $(3.2)$ を式 $(3.3)$ に代入すると、水素原子から放出される電磁波の波長を求めることができます。
$$ \begin{aligned} \lambda &= \frac{hc}{\left( -\frac{m q^4}{8\pi\varepsilon_0^2 h^2} \frac{1}{m^2} +\frac{m q^4}{8\pi\varepsilon_0^2 h^2} \frac{1}{n^2} \right)} \\ &\quad (m=1,2,3、n=m+1,m+2,\ldots) \end{aligned} $$リュードベリ定数を求めやすいように整理して逆数にすると、
$$ \begin{aligned} \frac{1}{\lambda} &= \frac{m q^4}{8\pi\varepsilon_0^2 h^3 c} \left( \frac{1}{m^2} -\frac{1}{n^2} \right) \\ &\quad (m=1,2,3、n=m+1,m+2,\ldots) \end{aligned} $$🌟 リュードベリ定数を求める
先ほどの式は式 $(3.1)$ と同じ形をしているので、係数を比較するとリュードベリ定数を求められます。
リュードベリ定数の定義
$$ \frac{1}{\lambda} = R\left( \frac{1}{m^2}-\frac{1}{n^2} \right) \quad (m=1,2,3、n=m+1,m+2,\ldots) $$先ほどの式
$$ \frac{1}{\lambda} = \frac{m q^4}{8\pi\varepsilon_0^2 h^3 c} \left( \frac{1}{m^2} -\frac{1}{n^2} \right) \quad (m=1,2,3、n=m+1,m+2,\ldots) $$リュドベる
$$ R = \frac{m q^4}{8\pi\varepsilon_0^2 h^3 c} $$実際に値を代入して計算してみます。
$$ \begin{aligned} m &: 9.11\times 10^{-31} \text{(kg)} \\ q &: 1.6\times 10^{-19} \text{(C)} \\ \varepsilon_0 &: 8.85\times 10^{-12} \text{(F/m)} \\ h &: 6.63\times 10^{-34} \text{(Js)} \\ c &: 3.0\times 10^8 \text{(m/s)} \\[1em] \end{aligned} $$$$ \begin{aligned} R &= \frac{(9.11\times 10^{-31})(1.6\times 10^{-19})^4}{8\pi(8.85\times 10^{-12})^2(6.63\times 10^{-34})^3(3.0\times 10^8)} \\[1em] &\approx 1.1\times 10^7 \text({m}^{-1}) \end{aligned} $$これは実験的に求められたリュードベリ定数 $R=1.097\times 10^7 \text{m}^{-1}$ とほぼ一致します。よって、ボーアの原子モデルは水素原子の発光スペクトルを説明できることを示せました。
ご覧いただきありがとうございました。