ソートアルゴリズムについてのまとめ
ソートアルゴリズム
計算量の違いまとめです。下の表は wiki にも載ってます。ここ
| 名称 | 最良 計算時間 | 平均 計算時間 | 最悪 計算時間 | 最悪 空間計算量 | 安定性 |
|---|---|---|---|---|---|
| バブルソート | $O(n)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 安定 |
| 選択ソート | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 不安定 |
| 挿入ソート | $O(n)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 安定 |
| マージソート | $O(n\log n)$ | $O(n\log n)$ | $O(n\log n)$ | $O(n)$ | 安定 |
| クイックソート | $O(n\log n)$ | $O(n\log n)$ | $O(n^2)$ | $O(\log n)$ | 不安定 |
| ヒープソート | $O(n\log n)$ | $O(n\log n)$ | $O(n\log n)$ | $O(1)$ | 不安定 |
計算量の覚え方は意外と簡単。まずは大まかに二種類に分類。上 3 つはいわば愚直策で二重ループを使っているため $O(n^2)$ になる(語弊アリ)。下 3 つは分割統治法を使っているため $O(n\log n)$ になる。その中で特徴的なやつを理由付けして覚えればいい。理由付けは後述してます。
安定不安定は、アルゴリズムの動作イメージを思い浮かべる必要がある。安定か不安定かは、隣り合う要素同士を交換するかどうかで決まる。隣り合う要素同士を交換する場合は安定、離れた要素同士を交換する場合は不安定。
用語の説明
安定性: ソート前のデータに同じ値が含まれるとき、ソート後にもその順序が保たれているかどうか。 例:
[ 3_b, 3_c, 1_a ] // ソート前 ↓ [ 1_a, 3_b, 3_c ] // 安定 [ 1_a, 3_c, 3_b ] // b, c の順序が入れ替わっているため不安定計算量: アルゴリズムの実行時間を表す指標。
最良計算時間: 入力データの中で最も早く処理される場合の計算量。例えばソート済みのデータが与えられた場合、バブルソートは $O(n)$ でソートできる。
最悪計算時間: 入力データの中で最も遅く処理される場合の計算量。例えばソート済みのデータが与えられた場合、クイックソートは $O(n^2)$ もかかる。
平均計算時間: これは面倒。考えられる入力データサイズを全て試し、かかる計算時間を求め平均時間を求める。データの並び順は確率的に決める。
空間計算量: アルゴリズムが必要とするメモリの量を表す指標。多分空間はメモリ空間の空間。
バブルソート
泡が上がっていくようにソートする。
最良計算時間が $O(n)$ なのが特徴。2 つめの for ループの中で一度もスワップがなければソートを終了する、といった最適化がなされている場合、$O(n)$ になる。
つまり次のコードは最良計算時間 $O(n)$ ではない。見にくくなるため、最適化を行わない場合のコードを載せている。最適化コードは後述。
降順になったデータを昇順にソートする場合、最適化をしても二重ループをフルに使ってスワップするため $O(n^2)$
隣同士のみで交換するため安定。
static void bubble_sort(int* p, int n)
{
for (int i = 0; i < n; ++i)
{
for (int j = n - 1; j > i; --j)
{
if (p[j] < p[j - 1])
{
std::swap(p[j], p[j - 1]);
}
}
}
}
i = 0 時の j, j-1 の変化イメージ。
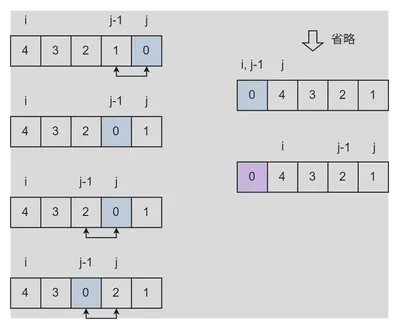
i の変化イメージ。
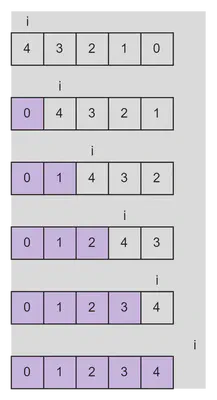
最適化を行った場合
static void bubble_sort(int* p, int n)
{
for (int i = 0; i < n; ++i)
{
bool is_un_swapped = true;
for (int j = n - 1; j > i; --j)
{
if (p[j] < p[j - 1])
{
std::swap(p[j], p[j - 1]);
is_un_swapped = false; // スワップがあった
}
}
if (is_un_swapped)
break; // スワップがなければ終了
}
}
選択ソート
最小値を線形探索して頭に持ってくるソート。
for ( $O(n)$ ) の中で線形探索 ( $O(n)$ ) を行うため $O(n^2)$ になる。ソート済みのデータが与えられた場合でも線形探索することになり早くならない。最良最悪平均共に $O(n^2)$ になる。
ここで、線形探索の最良計算時間は $O(1)$ じゃないの、と思うかもしれない。今回の場合、ある値を探索するのではなく、最小値を探すため、結局全ての要素を見る必要がある。よって線形探索の最良計算時間は $O(n)$ になる。
最小値を頭に持ってくるときに離れた要素同士を交換するため安定ではない。
static void selection_sort(int* p, int n)
{
for (int i = 0; i < n - 1; ++i)
{
// i から n の間で最小の値を探す
int minj = i;
for (int j = i; j < n; ++j)
{
if (p[j] < p[minj])
minj = j;
}
// 頭から順に入れ替え
std::swap(p[i], p[minj]);
}
}
挿入ソート
ソート済みのデータに新しいデータを挿入するイメージ。while の条件式に論理積があったりとソースコードが理解しにくいのでテストに出がち。許せんなぁ 動作を理解し解けばなんくるないさー
挿入ってあるから不安定だと思うかもしれないが、実は安定。隣り合う要素しか交換せず、かつ同じ値の場合は交換しないため。
最良計算時間が $O(n)$ なのが特徴。ソート済みのデータが与えられた場合、挿入する値は常にソート済み配列の末端に来るため、while する必要がなくなり $O(n)$ になる。
static void insert_sort(int* data, int n)
{
for (int i = 1; i < n; ++i)
{
int v = data[i]; // 挿入する値
int j = i - 1; // 挿入する末端位置 つまり、data[0] から data[i-1] まではソート済み
// 挿入位置を探索 挿入値がソート済みのデータの要素値より小さくなるまで探す (ソート済み配列を後ろから探索していくため)
while (j >= 0 && data[j] > v)
{
data[j + 1] = data[j]; // 挿入位置を空ける むんずむんず
--j;
}
data[j + 1] = v;
}
}
マージソート
todo
クイックソート
todo
ヒープソート
todo
ソート例題
穴あき問題が出て詰むのが定石なので、穴あき問題を解いてみる。
static void bubble_sort(int* p, int n)
{
for (int i = 0; i < n; ++i)
{
for (int j = n - 1; j > i; --j)
{
<???>
}
}
}
答え
if (p[j] < p[j - 1])
{
std::swap(p[j], p[j - 1]);
}
これは凶悪
static void insert_sort(int* data, int n)
{
for (int i = 1; i < n; ++i)
{
int v = data[i];
int j = i - 1;
while (<???>)
{
<???>
--j;
}
data[j + 1] = v;
}
}
答え
j >= 0 && data[j] > v
data[j + 1] = data[j];
static void bubble_sort(int* p, int n)
{
for (int i = 0; i < n; ++i)
{
bool is_un_swapped = true;
for (int j = n - 1; j > i; --j)
{
if (p[j] < p[j - 1])
{
std::swap(p[j], p[j - 1]);
<???>
}
}
<???>
}
}
答え
is_un_swapped = false;
if (is_un_swapped)
break;
static void bubble_sort(int* p, int n)
{
for (int i = 0; i < n; ++i)
{
for (<???>)
{
if (p[j] < p[j - 1])
{
std::swap(p[j], p[j - 1]);
}
}
}
}
答え
int j = n - 1; j > i; --j